[最も共有された! √] p(x) formula polynomial 248734-P(x) formula polynomial
Let us take an example of the polynomial p(x) of degree 1 as given below p(x) = 5x 1 According to the definition of roots of polynomials, 'a' is the root of a polynomial p(x), if P(a) = 0 Thus, in order to determine the roots of polynomial p(x), we have to find the value of x for which p(x) = 0 Now, 5x 1 = 0 x = 1/5Polynomial functions are the most easiest and commonly used mathematical equation It can be expressed in terms of a polynomial The polynomial equation is used to represent the polynomial function Generally, a polynomial is denoted as P(x) The greatest exponent of the variable P(x) is known as the degree of a polynomialIf x= p q is a rational solution to the polynomial equation f(x) = 0 then qx pis a factor of the polynomial f(x) and so we can use long division to write f(x) = (qx p)g(x) where g(x) is a polynomial of smaller degree We teach a version of this method in high school when students learn to solve quadratic equations by factoring

Properties Of Roots Of Polynomials Mathematics Stack Exchange
P(x) formula polynomial
P(x) formula polynomial-If P(x) is a polynomial in x and k is any real number, then the value of P(k) at x = k is denoted by P(k) is found by replacing x by k in P(x) Example 2 In the polynomial x 2 – 3x 2, Replacing x by 1 gives, P(1) = 1 – 3 2 = 0 Similarly, replacing x by 2 gives, P(2) = 462 = 0 For a polynomial P(x), real number kF(x) =4x³2x²8x21 and g(x) =7x²3x12 are polynomials in variable x whereas p(y) =2y²3y4 is a polynomial in a variable y 7x³2x²3√x is not considered as a polynomial because the exponent of x in 3√x is not a positive integer


Arxiv Org Pdf 1309 3934
Free polynomial equation calculator Solve polynomials equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyF(x) =4x³2x²8x21 and g(x) =7x²3x12 are polynomials in variable x whereas p(y) =2y²3y4 is a polynomial in a variable y 7x³2x²3√x is not considered as a polynomial because the exponent of x in 3√x is not a positive integerFind the polynomial of least degree containing all of the factors found in the previous step
The graph is shown at right using the WINDOW (5, 5) X (8, 8) The maximum point is found at x = 1 and the maximum value of P(x) is 3 The coordinates of this point could also be found using the calculator Polynomials of degree greater than 2 Polynomials of degree greater than 2 can have more than one max or min value(Yes, "5" is a polynomial, one term is allowed, and it can be just a constant!) These are not polynomials 3xy2 is not, because the exponent is "2" (exponents can only be 0,1,2,);If P(x) is a polynomial in x and k is any real number, then the value of P(k) at x = k is denoted by P(k) is found by replacing x by k in P(x) Example 2 In the polynomial x 2 – 3x 2, Replacing x by 1 gives, P(1) = 1 – 3 2 = 0 Similarly, replacing x by 2 gives, P(2) = 462 = 0 For a polynomial P(x), real number k
Example 2x 3 −x 2 −7x2 The polynomial is degree 3, and could be difficult to solve So let us plot it first The curve crosses the xaxis at three points, and one of them might be at 2We can check easily, just put "2" in place of "x"How To Given a graph of a polynomial function, write a formula for the function Identify the xintercepts of the graph to find the factors of the polynomial;The calculator accepts both univariate and multivariate polynomials Show Instructions In general, you can skip the multiplication sign, so `5x` is equivalent to `5*x` In general, you can skip parentheses, but be very careful e^3x is `e^3x`, and e^(3x) is `e^(3x)`



Zeros Of Polynomials Matching Equation To Graph Video Khan Academy



Proof That There Exists Irreducible Polynomial Of Degree N Mathematics Stack Exchange
The polynomial of degree 5, P(x) has leading coefficient 1, has roots of multiplicity 2 at x=1 and x=0, and a root of multiplicity 1 at x=3, how do you find a possible formula for P(x)?If a polynomial contains a factor of the form (x−h)p (x − h) p, the behavior near the x intercept h is determined by the power p We say that x =h x = h is a zero of multiplicity p The graph of a polynomial function will touch the x axis at zeros with even multiplicities The graph will cross the x axis at zeros with odd multiplicitiesA polynomial function is a function that can be expressed in the form of a polynomial The definition can be derived from the definition of a polynomial equation A polynomial is generally represented as P (x) The highest power of the variable of P (x) is known as its degree


Projecteuclid Org Download Pdfview 1 Euclid Aop


Q Tbn And9gct8mayrutblihfrij Exgx Irodhpeygrmtrqpn8xb76v23tkjt Usqp Cau
Introduction to Polynomial Equation If p (x) is a polynomial equation in x, then the highest power of x in p (x) is called the degree of the polynomial p (x) So, p (x) = 4x 2 is a polynomial equation in the variable x of degree 1If a polynomial of lowest degree p has zeros at x= x1,x2,,xn x = x 1, x 2, , x n, then the polynomial can be written in the factored form f (x) = a(x−x1)p1(x−x2)p2 ⋯(x−xn)pn f (x) = a (x − x 1) p 1 (x − x 2) p 2 ⋯ (x − x n) p n where the powers pi p i on each factor can be determined by the behavior of the graph at the corresponding intercept, and the stretch factor a can be determined given a value of the function other than the x interceptGiven a set of n 1 data points (x i, y i) where no two x i are the same, one is looking for a polynomial p of degree at most n with the property =, =, , The unisolvence theorem states that such a polynomial p exists and is unique, and can be proved by the Vandermonde matrix, as described below


Rational Zeros Of Polynomials



Finding Zeros Of Polynomials 1 Of 2 Video Khan Academy
The Remainder Theorem starts with an unnamed polynomial p(x), where "p(x)" just means "some polynomial p whose variable is x" Then the Theorem talks about dividing that polynomial by some linear factor x – a, where a is just some numberAlgebra > Polynomialsandrationalexpressions> SOLUTION The polynomial of degree 4, P ( x ) has a root of multiplicity 2 at x = 3 and roots of multiplicity 1 at x = 0 and x = − 2 It goes through the point ( 5 , 56 ) Find a formula Log OnExamine the behavior of the graph at the xintercepts to determine the multiplicity of each factor;



Polynomial Graphs Mathbitsnotebook Ccss Math


Www Jstor Org Stable
Constant polynomial is a function of the form p(x)=c for some number c For example, p(x)=5 3 or q(x)=7 The output of a constant polynomial does not depend on the input (notice that there is no x on the right side of the equation p(x)=c) Constant polynomials are also called degree 0 polynomials The graph of a constant polynomial is aUsing your notation, we know that the product p (x) q (x) is a polynomial of degree n mQuestion The polynomial of degree 5, P(x) has leading coefficient 1, has roots of multiplicity 2 at x=1 and x=0, and a root of multiplicity 1 at x=−3 Find a possible formula for P(x) P(x)= Answer by Alan3354() (Show Source)



Answered The Polynomial Of Degree 5 P X Has Bartleby



Solved The Polynomial Of Degree 4 P X Has A Root Of Mul Chegg Com
2/(x2) is not, because dividing by a variable is not allowed 1/x is not either √x is not, because the exponent is "½" (see fractional exponents);Click here👆to get an answer to your question ️ Let p(x) = 0 be a polynomial equation of least possible degree, with rational coefficients, having 7^1/3 49^1/3 as one of its roots Then the product of all the roots of p(x) = 0 isLet us take an example of the polynomial p(x) of degree 1 as given below p(x) = 5x 1 According to the definition of roots of polynomials, 'a' is the root of a polynomial p(x), if P(a) = 0 Thus, in order to determine the roots of polynomial p(x), we have to find the value of x for which p(x) = 0 Now, 5x 1 = 0 x = 1/5


Let P X Be A Cubic Polynomial And Alpha Beta Gamma Are Roots Of Equation P X 0 If Youtube


Http Www Math Lsa Umich Edu Karni M471 Hw6 Pdf
Polynomial Division Calculator Step 1 Enter the expression you want to divide into the editor The polynomial division calculator allows you to take a simple or complex expression and find the quotient and remainder instantly Step 2 Click the blue arrow to submit and see the result!Click here👆to get an answer to your question ️ Let p(x) = 0 be a polynomial equation of least possible degree, with rational coefficients, having 7^1/3 49^1/3 as one of its roots Then the product of all the roots of p(x) = 0 isOnce you've got some experience graphing polynomial functions, you can actually find the equation for a polynomial function given the graph, and I want to try to do that now So this one is a cubic We're calling it f(x), and so, I want to write a formula for f(x) Now let me start by observing that the x intercepts are 3, 1, and 2
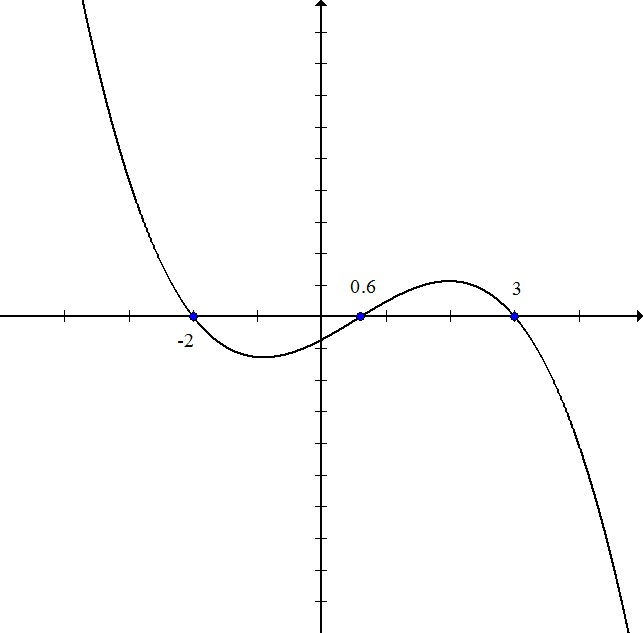


Write The Equation Of A Polynomial Function Based On Its Graph Precalculus
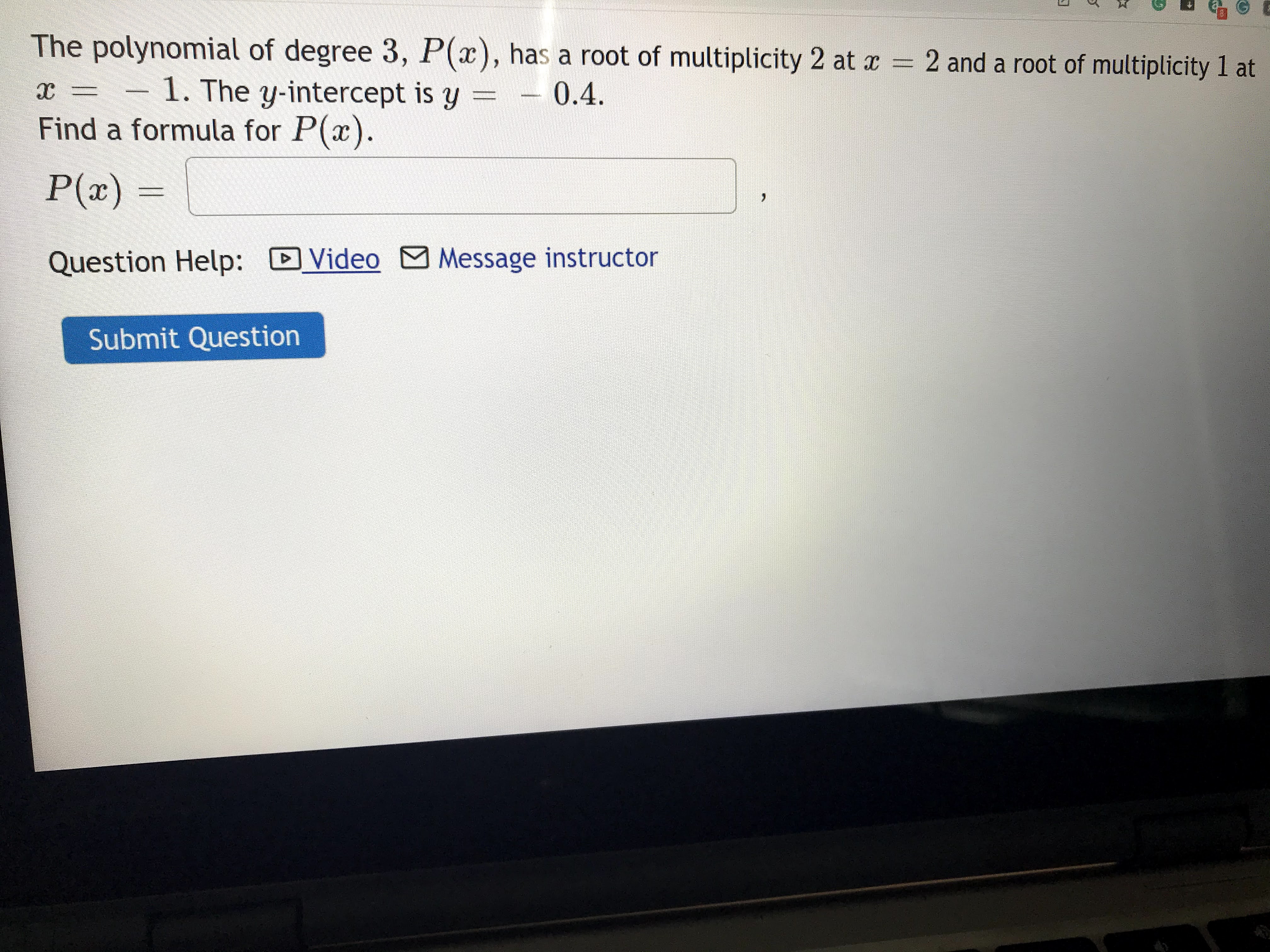


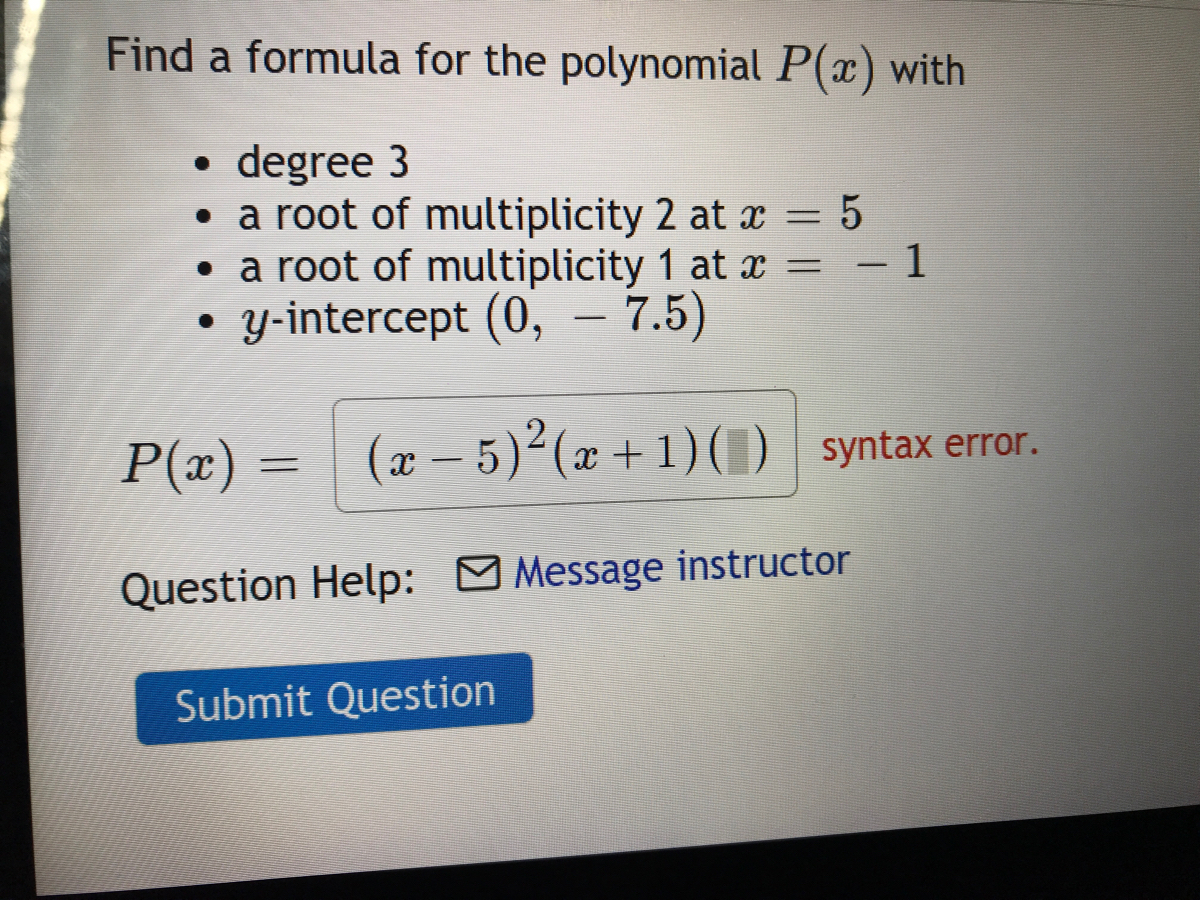
Answered The Polynomial Of Degree 3 P X Has A Bartleby
Solution x 2 25 = (x 5)(x 5) => we have to solve the following 2 equations x 5 = 0 or x 5 = 0 so the equation have two decisions x = 5 and x = 5 Related Resources Polynomial identities quiz Simplifying polynomial expressions problems with solutions Factoring polynomials problems with solutions Polynomial identities in theBut these are allowed x/2 is allowed, because you canPolynomial factoring calculator This online calculator writes a polynomial as a product of linear factors Able to display the work process and the detailed step by step explanation



Polynomial And Its Types Polynomial Equation Concepts Zeroes So On


Legendre Polynomials
Algebra > Polynomialsandrationalexpressions> SOLUTION The polynomial of degree 4, P ( x ) has a root of multiplicity 2 at x = 3 and roots of multiplicity 1 at x = 0 and x = − 2 It goes through the point ( 5 , 56 ) Find a formula Log OnZero polynomial A polynomial consisting of one term, namely zero only is called a zero polynomialThe degree of zero polynomial is not defined Zeroes of a polynomial Let p(x)be a polynomial If then we say that is zero of the polynomial of p(x) Remark Finding the zeroes of polynomial p(x) means solving the equation p(x)=0Question The polynomial of degree 5, P ( x ) has leading coefficient 1, has roots of multiplicity 2 at x = 2 and x = 0 , and a root of multiplicity 1 at x = − 2 Find a possible formula for P ( x ) P(x)= Found 2 solutions by Boreal, ikleyn


2


Polynomials Class 10th Formulas Studyrankersonline
The polynomial of degree 4, P(x) has a root of multiplicity 2 at x=3 and roots of multiplicity 1 at x=0 and x=3A Polynomial can be expressed in terms that only have positive integer exponents and the operations of addition, subtraction, and multiplication In other words, it must be possible to write the expression without division It's easiest to understand what makes something a polynomial equation by looking at examples and non examples as shown belowSOLUTION The polynomial of degree 5, P (x) has leading coefficient 1, has roots of multiplicity 2 at x = 2 and x = 0, and a root of multiplicity 1 at x = − 2 Find a possible formula fo



Quadratic Function Wikipedia



Sum And Product Of Zeros In Quadratic Polynomial Solved Examples Algebra Cuemath
Polynomial factoring calculator This online calculator writes a polynomial as a product of linear factors Able to display the work process and the detailed step by step explanationZero polynomial A polynomial consisting of one term, namely zero only is called a zero polynomialThe degree of zero polynomial is not defined Zeroes of a polynomial Let p(x)be a polynomial If then we say that is zero of the polynomial of p(x) Remark Finding the zeroes of polynomial p(x) means solving the equation p(x)=0Univariate Polynomial A univariate polynomial has one variable—usually x or tFor example, P(x) = 4x 2 2x – 9In common usage, they are sometimes just called "polynomials" For realvalued polynomials, the general form is p(x) = p n x n p n1 x n1 p 1 x p 0 The univariate polynomial is called a monic polynomial if p n ≠ 0 and it is normalized to p n = 1 (Parillo



2 9 Solving Polynomial Equations



Solved 1 Find A Formula For The Polynomial P X With Deg Chegg Com
A negative zero of p(x), if exists, is a positive zero of p(−x) The number of real negative zeros of p(x) is related to the number of sign changes in the coefficients of p(−x) Example 1 Consider the polynomial p(x) = x4 2x2 −x −1 Then v = 1, so n p is either 0 or 1 by rule (i) But by rule (ii) v −n p must be even Hence n p = 1Question The polynomial of degree 4, P(x) has a root of multiplicity 2 at x=4 and roots of multiplicity 1 at x=0 and x=4 It goes through the point (5,45) Find a formula for P(x) Answer by josgarithmetic() (Show Source)Example of polynomial function f(x) = 3x 2 5x 19 Read More Polynomial Functions Polynomial Equations Formula Usually, the polynomial equation is expressed in the form of a n (x n) Here a is the coefficient, x is the variable and n is the exponent


Http Mathstat Carleton Ca Ckfong Hs13a Pdf


2
Constant polynomial is a function of the form p(x)=c for some number c For example, p(x)=5 3 or q(x)=7 The output of a constant polynomial does not depend on the input (notice that there is no x on the right side of the equation p(x)=c) Constant polynomials are also called degree 0 polynomials The graph of a constant polynomial is aPolynomial Equation A singlevariable polynomial having degree n has the following equation a n x n a n1 x n1 a 2 x 2 a 1 x 1 a 0 x 0 In this, a's denote the coefficients whereas x denotes the variable Since x 1 = x and x 0 = 1 considering all complex numbers x Therefore, the above expression can be shortened to a n x nQuestion The polynomial of degree 5, P(x) has leading coefficient 1, has roots of multiplicity 2 at x=1 and x=0, and a root of multiplicity 1 at x=−3 Find a possible formula for P(x) P(x)= Answer by Alan3354() (Show Source)
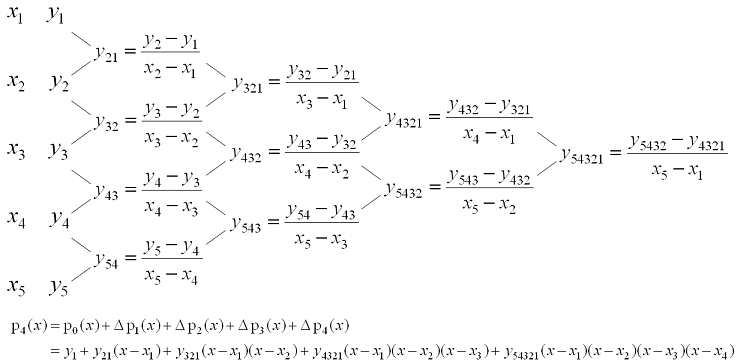


5 3 Newton Polynomials Department Of Electrical And Computer Engineering University Of Waterloo



Solved 2 A Find A Polynomial P X Of Degree 2 That Chegg Com
Division Algorithm For Polynomials With Examples Example 1 Divide 3x 3 16x 2 21x by x 4 Sol Quotient = 3x 2 4x 5 Remainder = 0 Example 2 Apply the division algorithm to find the quotient and remainder on dividing p(x) by g(x) as given below p(x) = x 3 – 3x 2 5x – 3 and g(x) = x 2 – 2 Sol We have, p(x) = x 3 – 3x 2 5x – 3 and g(x) = x 2 – 2P (x) P (x) is equal to zero Finding the roots of a polynomial is sometimes called solving the polynomialA Polynomial can be expressed in terms that only have positive integer exponents and the operations of addition, subtraction, and multiplication In other words, it must be possible to write the expression without division It's easiest to understand what makes something a polynomial equation by looking at examples and non examples as shown below



Equation Of A Polynomial Function Solutions Examples Videos Worksheets Activities


Answered The Polynomial Of Degree 5 P X Has Bartleby
A polynomial P(x) divided by Q(x) results in R(x) with zero remainders if and only if Q(x) is a factor of P(x) the constant term An example of a polynomial equation is b = a 4 3a 32a 2 a 1 Polynomial Functions A polynomial function is an expression constructed with one or more terms of variables with constant exponents If thereIn order to determine an exact polynomial, the "zeros" and a point on the polynomial must be provided Examples Practice finding polynomial equations in general form with the given zeros Find an* equation of a polynomial with the following two zeros = −2, =4 Step 1 Start with the factored form of a polynomialPOLYNOMIALS (Polynomials with Real Coefficients) Definition 1 A real polynomial is an expression of the form P(x) = anxn an−1xn−1 ···a1xa0 where n is a nonnegative integer and a0,a1,,an−1,anare real numbers with an6= 0 The nonnegative integer n is called the degree of P The numbers a0,a1,,an−1,an



Zero Of The Polynomial P X 2x 5 Is Youtube



Factoring Using Polynomial Division Video Khan Academy


Q Tbn And9gcts05mgre9ll1wp96m6ddtcfwe6vpmr5 4cxol6q2vg3plrgr3k Usqp Cau



Polynomials Sums And Products Of Roots



28 Mac Laurin Expansions X


2



Solved Find A Formula For The Polynomial P X With Degree Chegg Com


Polynomials Definition Types And Examples


Answered Find A Formula For The Polynomial P X Bartleby


Q Tbn And9gcr jxguchitceu1gjvqxb 8nad7s2roinis8nyt Quim34c4q Usqp Cau



Cyclotomic Polynomial Wikipedia



Give Examples Of Polynomials P X G X Q X And R X Which Satisfy The Division Algorithm And I Deg P X Deg Q X Ii Deg Q X Deg R X Iii Deg R X 0


Finding The Formula For A Polynomial Given Zeros Roots Degree And One Point Example 1 Youtube



Solved Find A Formula For The Polynomial P X With Degr Chegg Com
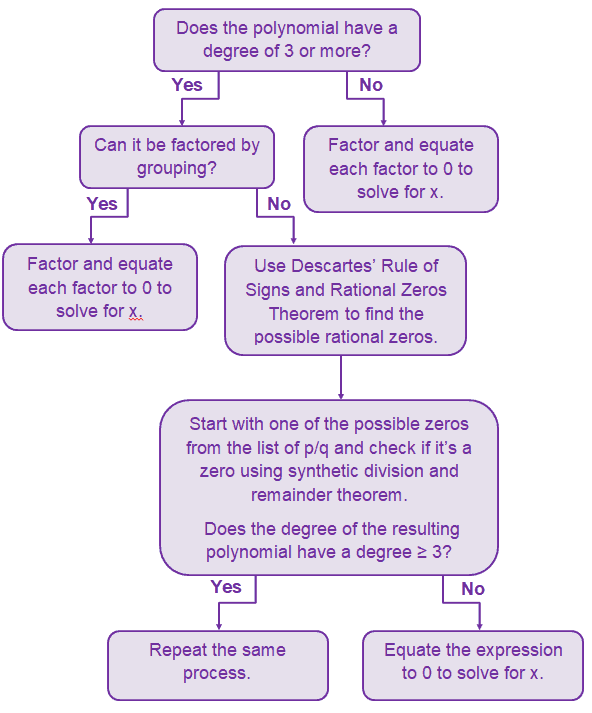


Polynomial Equation Properties Techniques And Examples



Cbse 10 Maths Polynomials Relationship Between Zeroes And Coefficient Of A Polynomial Study Material


Faculty Math Illinois Edu Pat Sp07 Taylor Pdf


Q Tbn And9gcssybq V6w5c4ycihm 68bcxq8mejb95tggv4bgo Rjkxe7bjcq Usqp Cau


Victoriakala Files Wordpress Com 19 04 Math4b W16 Factoringcubicpolynomials Pdf



Properties Of Roots Of Polynomials Mathematics Stack Exchange



Solved 28 A Find A Polynomial P X Of Degree S 2 That Chegg Com



The Polynomial Of Degree 3 P X Has A Root Of Multiplicity 2 At X 1 And A Root Of Multiplicity 1 At X 5 The Y Interc Homeworklib



Polynomial Theorems Faculty Lasierra Edu



Zeros Of P X


2



Verify Division Algorithm For The Polynomials Br P X 3x


2



Remainder Theorem Remainder Theorem Of Polynomial Examples



The Zeros Of The Polynomial P X X 2 X 6 Are Youtube
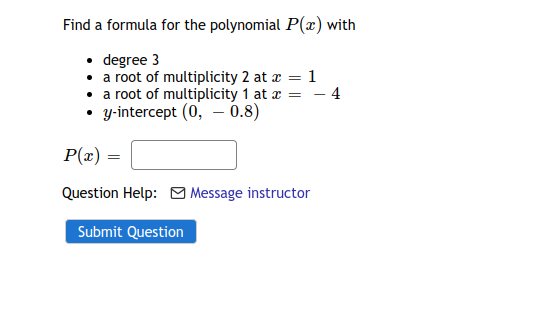


Answered Find A Formula For The Polynomial P X Bartleby


Http Math Cmu Edu Cargue Arml Archive 17 18 Algebra 09 10 17 Pdf


Solution Sketch A Cubic Function Third Degree Polynomial Function Y P X With Two Distinct Zeros At X 2 And X 5 And Has A Local Maximum Located At X 5 Then Determine A Formula For Your
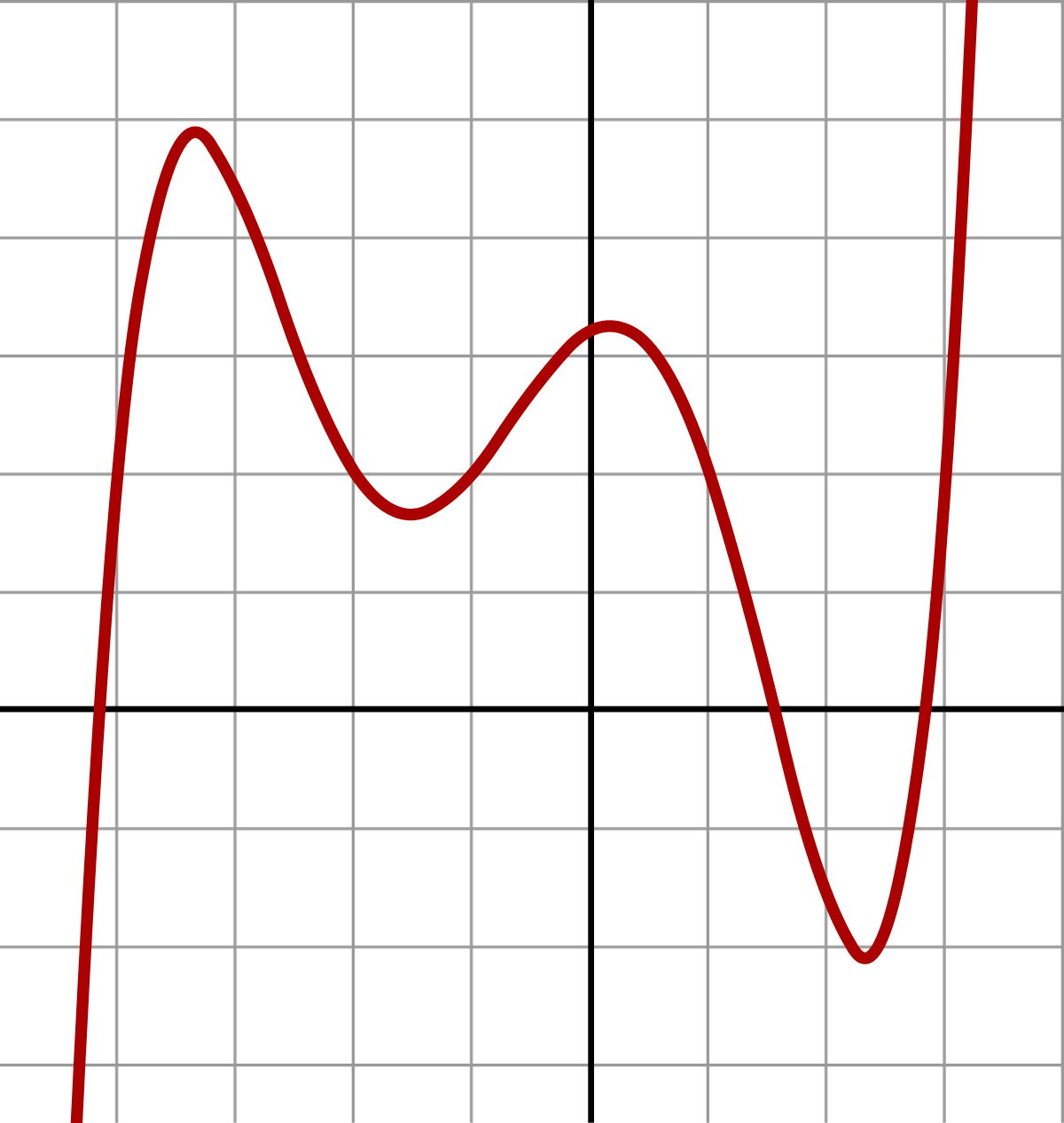


Quintic Function Wikipedia
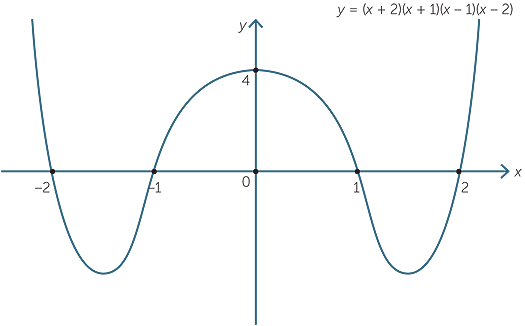


Polynomials



Equation Of A Polynomial Given The Zeros And A Point 143 3 7 2 A Youtube



Polynomial Functions



Cbse Class 10 Maths Chapter 2 Polynomials Formula



Answered Find A Formula For The Polynomial P X Bartleby
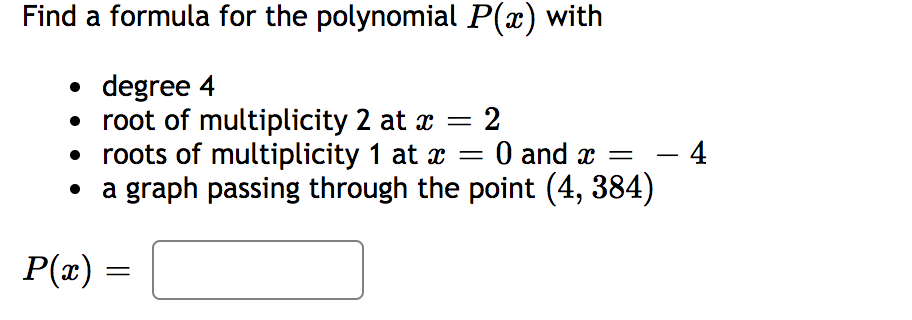


Solved Find A Formula For The Polynomial P X With Degr Chegg Com


Rational Zeros Of Polynomials
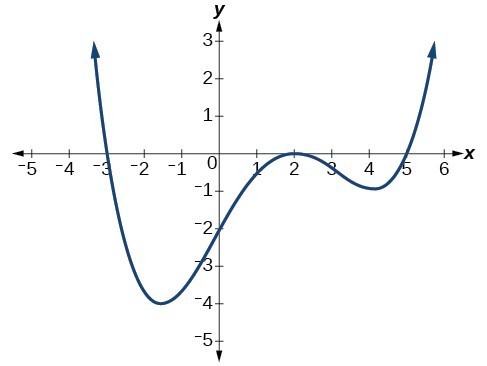


Writing Formulas For Polynomial Functions College Algebra
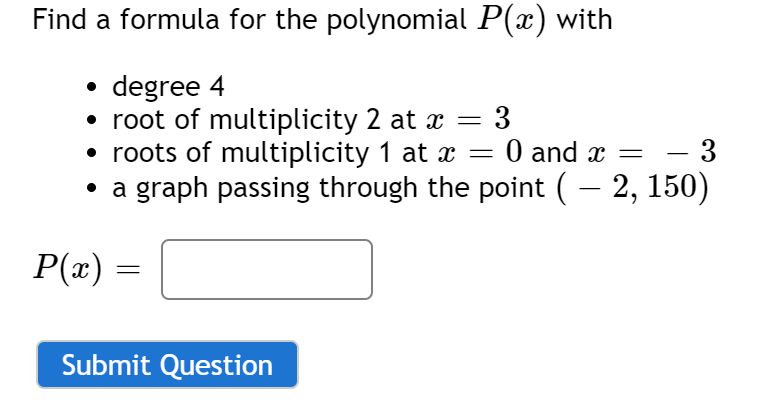


Solved Find A Formula For The Polynomial P X With Degree Chegg Com



Solving Cubic Equations Solutions Examples Videos


View Question The Polynomial Of Degree 5 P X Has Leading Coefficient 1 Has Roots Of Multiplicity 2 At X 5 And X 0 And A Root Of Multiplicity 1 At X 5


Arxiv Org Pdf 1309 3934



Find The Value Of K If X 1 Is A Factor Of P X In The Given Equations Youtube
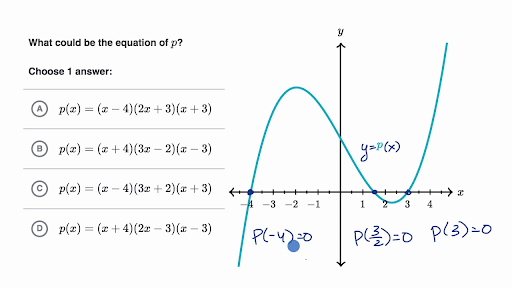


Zeros Of Polynomials Matching Equation To Graph Video Khan Academy


Polynomial Function



Equation Solver Wolfram Alpha


Writing Formulas For Polynomial Functions College Algebra



Forming Polynomial Equations With Roots Video Lesson Transcript Study Com



7 5 Polynomial Equations And Applications Hunter College Math101


2


Core Ac Uk Download Pdf Pdf


Http Www Pstcc Edu Facstaff Rtjackso Math1710 Worksheets Approx Polynomials Pdf


Yisun Io Notes Polynomials Pdf


Solution The Polynomial Of Degree 3 P X Has A Root Of Multiplicity 2 At X 4 And A Root Of Multiplicity 1 At X Amp 8722 4 The Y Intercept Is Y Amp 8722 51 2 Find A Formula For P X



Polynomial Wikipedia



7 Ways To Factor Second Degree Polynomials Quadratic Equations
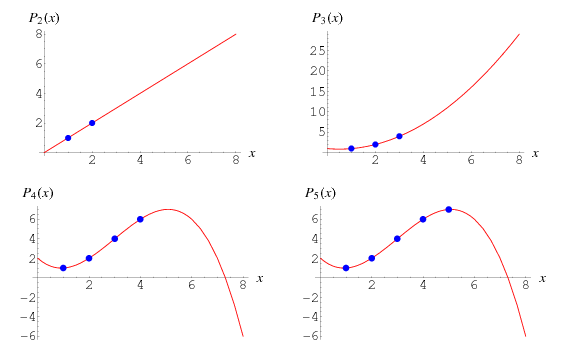


Lagrange Interpolating Polynomial From Wolfram Mathworld



Vieta S Formulas Wikipedia



Number Of Possible Real Roots Of A Polynomial Video Khan Academy


Polynomial Wikipedia



Polynomial Division Calculator


Www Colorado Edu Amath Sites Default Files Attached Files Interpolation Pdf


Arxiv Org Pdf 1504



Polynomial Functions



Solved I Show There Is A Unique Cubic Polynomial P X Fo Chegg Com


Alexanderrem Weebly Com Uploads 7 2 5 6 Polynomials Pdf


How To Prove That The Polynomial Math P X X 3 X 2 2x 1 Math Has Only Real Roots Quora


Http Www Math Ucsd Edu Hwenzl Orderthree Pdf



Suppose The Quadratic Polynomial P X Ax2 Bx C Has Positive Coeffieicents A B C In Arithmentic Progression In That Order If P X 0 Has Integer Roots A A Mathematics Topperlearning Com Yqunpd55



Pdf Bivariate Fibonacci And Lucas Like Polynomials


Polynomial Equation Mathematics Britannica



Factoring Higher Degree Polynomials Video Khan Academy
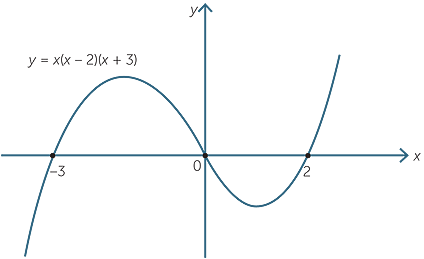


Polynomials


コメント
コメントを投稿